CircuiTikZと伝送線路

最近、LateXの回路図作成パッケージ circuitikzを使って回路図を作成することがある。CUIベースで論文にも使えるようなきれいな回路図が書ける。（こういうの学部生の時に学んでおきたかった。）

マニュアルはコチラ

絶対座標か相対座標を使って描画する。複雑な回路は相対座標の方が便利。描画したいコンポーネントを座標で囲んで描画する。配線は以下のように–で描画できる。

\draw (0,0) -- (2,0);
\draw (0,2) -- ++(2,0);

上が絶対座標、下が相対座標を使って描画している。以下のような同じ結果が得られる。

to[]を使えばR, L, C等の受動・能動コンポーネントを描画できる。

\begin{circuitikz}[]
\draw (0,0) to[R,*-*]++(2,0);
\end{circuitikz}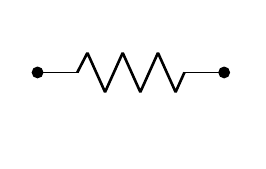

詳しくはマニュアルを参照。今回はcircuitikzを使って伝送線路の電信方程式(Telegraph Equation)を描いてみた。コードは本記事の最後に載せておく。

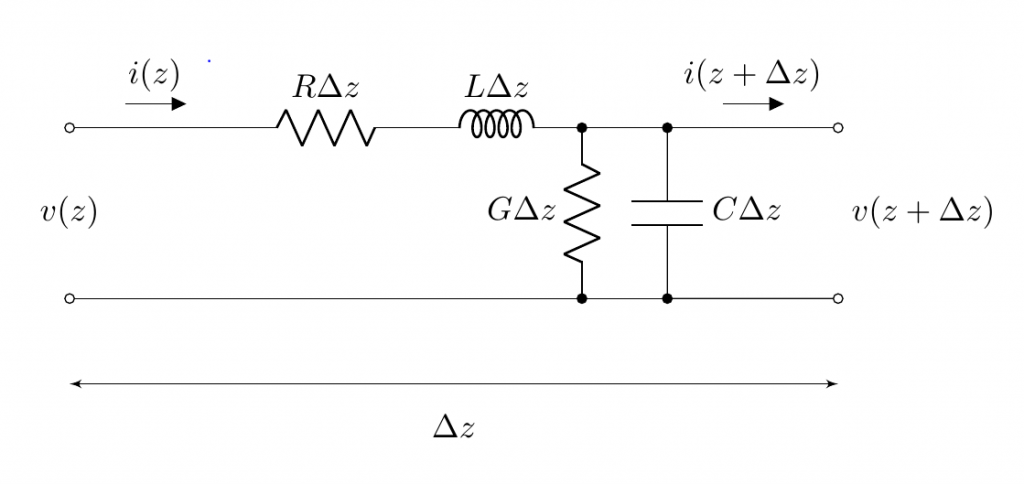
R, L, G, Cはそれぞれ単位長さあたりの値。つまり電界と磁界が交差しながら伝わる伝送線路において断面構造の電界、磁界分布と伝送媒質（導体、誘電体）特性から求まる。

電信方程式からは、伝送線路の伝搬特性を表す特性インピーダンス、伝播定数（実部：減衰定数、虚部：位相定数）が以下のように得られる。

\begin{eqnarray} Z_{0} = \sqrt{\frac{(R + j\omega L)}{(G + j\omega C)}}\\ \gamma_{0} = \alpha + j\beta = \sqrt{(R + j \omega L)(G + j\omega C)} \end{eqnarray}

これらが分かれば、等価回路上で伝送線路として扱うことができる。インピーダンス整合、共振器、アンテナ、フィルタ等の設計には必須。基本的な伝送線路、例えば単一誘電体からなる同軸線路、マイクロストリップ、平衡平板等は静電磁界分布を求めることにより解析的にR, L, G, Cを求めることができる。（それらについてはたぶんまた別の記事を書く）

circuitikzにはRF回路でよく使われるようなアンテナ、伝送線路、増幅器、混合器等々のコンポーネントもパッケージ内に用意されている。scikit-rfと合わせて今後紹介していきたい。

\begin{circuitikz}[]
\draw (0,0)to[short,o-,f=$i(z)$]++(2,0) to[R=$R\Delta z$] ++(2,0)to[L=$L\Delta z$] ++(2,0)coordinate(Branch);
\draw (Branch)to[R,l_=$G\Delta z$,*-*] ++(0,-2)to [short,-o] ++(-6,0);
\draw (Branch)to[short ,o-o] ++(1,0) coordinate(Branch2)to[short,-o,f=$i(z + \Delta z)$]++(2,0);
\draw (Branch2)to[C=$C\Delta z$,*-*] ++(0,-2) coordinate(Branch3) to [short,-o]++(2,0);
\draw(Branch3) -- ++(-1,0);
\draw (0,-1)node{$v(z)$};
\draw (10,-1)node{$v(z + \Delta z)$};
\draw [latexslim-latexslim] (0,-3) -- (9,-3);
\draw (4.5,-3.5)node{$\Delta z$};
\end{circuitikz}